

क्रिकेटची विश्वचषक स्पर्धा सुरू झाली आहे. या स्पर्धेतल्या काही सामन्यांना पावसाचा फटका बसण्याची शक्यता आहे. अशा वेळी धावसंख्येचे लक्ष्य निश्चित करण्यासाठी डकवर्थ/ लुईस/स्टर्न यांनी सुचवलेल्या गणिती नियमाचा वापर केला जाईल. गणितावर आधारलेल्या अशा विविध नियमांची ही ओळख…
मराठी विज्ञान परिषदेच्या ‘पत्रिका’ या मासिकातील विवेक पाटकर यांचा हा पूर्वप्रकाशित लेख
क्रिकेट हा जगातील निवडक देशांत खेळला जाणार खेळ असला, तरी त्याचा रंजक इतिहास आणि लोकप्रियता वादातीत आहे. पाच दिवसांचा म्हणजे सुमारे साडेचारशे षटकांचा कसोटी सामना ते एकदिवसीय म्हणजे एकूण शंभर षटकांचा सामना, व त्यानंतर टी२० म्हणजे एकूण ४० षटकांचा सामना, अशी त्यात कालानुरूप स्थित्यंतरे घडत गेली आहेत. मात्र, साधारणपणे या सर्व प्रकारच्या आंतरराष्ट्रीय क्रिकेट सामन्यांना प्रेक्षकांची भरपूर गर्दी होते. दूरचित्रवाणीमुळे जागतिक पातळीवर अशा सामन्यांचा मागोवा सतत घेतला जातो. ‘सभ्य लोकांचा संथ खेळ’ अशी एके काळी प्रतिमा असणारा हा खेळ, आता गतिमान झाला असून मोठ्या आर्थिक उलाढालीचे केंद्रही बनला आहे.
अशा एखाद्या सामन्यात पावसामुळे व्यत्यय आल्यास प्रेक्षकांचा हिरमोड होऊ शकतो, तसेच संयोजकांचे आर्थिक नुकसानही होऊ शकते. ही बाब मर्यादित षटकांच्या सामन्यांसाठी तर कळीची ठरते, मुख्यतः एखाद्या निर्णायक सामन्यासाठी! अशा व्यत्ययानंतर खेळ सुरू झाल्यास खेळाची षटके कमी केली जातात. त्यामुळे विजयासाठी मूळ लक्ष्य बदलून नवे लक्ष्य ठरवणे भाग पडते. त्यासाठी वेळोवेळी काही गणिती पद्धती वापरल्या गेल्या आहेत. त्यांतील एआरआर (अॅव्हरेज रन रेट) ही एक पद्धत आहे. खेळात व्यत्यय आल्यास, या पद्धतीनुसार दर षटकामागे धावांची सरासरी ज्या संघाची जास्त असेल, तो संघ विजेता ठरे. मात्र या पद्धतीचा फायदा बऱ्याच वेळा, नंतर फलंदाजी करणाऱ्या संघाला मिळे. कारण, त्यास आपल्या धावांची गती किती पाहिजे हे नक्की माहीत असल्याने त्या संघाचा खेळ सुरुवातीपासूनच त्या दृष्टीनेच झालेला असे.
 सामना कमी षटकांचा झाल्यास वापरली जाणारी दुसरी पद्धत म्हणजे एमपीओ (मॅक्झिमम प्रॉडक्टिव्ह ओव्हर्स). या दुसऱ्या पद्धतीत नंतर फलंदाजी करणाऱ्या संघाचे पुनः ठरवले गेलेले लक्ष्य, हे त्याला जितकी षटके आता मिळणार आहेत तवेढीच, पण पहिल्या संघाने जास्तीतजास्त धावा काढलेली षटके विचारात घेऊन ते ठरवले जात असे. यात साधारणपणे प्रथम फलंदाजी करणाऱ्या संघाला फायदा मिळे. कारण, या पद्धतीनुसार दुसऱ्या संघाला काही वेळा अतिजलद खेळावे लागत असे. या पद्धतीचा फटका बसलेले उत्तम उदाहरण म्हणजे १९९२मधील एकदिवसीय विश्वचषक स्पर्धेच्या उपांत्य फेरीचा सामना. या सामन्यात दक्षिण आफ्रिकेला पावसानंतर इंग्लंडविरुद्ध विजयासाठी एका चेंडूत २२ धावा काढण्याचे लक्ष्य मिळाले होते, जे अर्थातच अशक्यप्राय होते.
सामना कमी षटकांचा झाल्यास वापरली जाणारी दुसरी पद्धत म्हणजे एमपीओ (मॅक्झिमम प्रॉडक्टिव्ह ओव्हर्स). या दुसऱ्या पद्धतीत नंतर फलंदाजी करणाऱ्या संघाचे पुनः ठरवले गेलेले लक्ष्य, हे त्याला जितकी षटके आता मिळणार आहेत तवेढीच, पण पहिल्या संघाने जास्तीतजास्त धावा काढलेली षटके विचारात घेऊन ते ठरवले जात असे. यात साधारणपणे प्रथम फलंदाजी करणाऱ्या संघाला फायदा मिळे. कारण, या पद्धतीनुसार दुसऱ्या संघाला काही वेळा अतिजलद खेळावे लागत असे. या पद्धतीचा फटका बसलेले उत्तम उदाहरण म्हणजे १९९२मधील एकदिवसीय विश्वचषक स्पर्धेच्या उपांत्य फेरीचा सामना. या सामन्यात दक्षिण आफ्रिकेला पावसानंतर इंग्लंडविरुद्ध विजयासाठी एका चेंडूत २२ धावा काढण्याचे लक्ष्य मिळाले होते, जे अर्थातच अशक्यप्राय होते.
काही काळ डीएमपीओ (डिस्काउण्टेड मॅक्झिमम प्रॉडक्टिव ओव्हर्स) ही पद्धत वापरात होती. ही पद्धत वर उल्लिखित एमपीओ पद्धतीची थोडी सुधारित आवृत्ती होती. यात एमपीओ पद्धतीने काढलेले, दुसऱ्या संघासाठीचे धावांचे लक्ष्य थोड्या टक्क्यांनी कमी केले जायचे. दुसऱ्या संघावरील अन्याय कमी करण्याचा हा अर्धवट प्रयत्न होता. १९९६च्या एकदिवसीय क्रिकेट विश्वचषक स्पर्धेत एक अन्वस्तीय (म्हणजे पॅरॅबोलिक) गणिती सूत्र मांडून लक्ष्य ठरवण्याची पद्धत (पीएआरएबी) वापरली गेली. ती पद्धत १९९५मध्ये डब्ल्यू. दो रेगो या साउथ आफ्रिकन गणितज्ञाने सुचविली होती. या पद्धतीत वापरले गेलेले सूत्र हे उर्वरित षटके आणि हव्या असलेल्या धावा यांवर आधारलेले होते. या सूत्राचा वापर करून दुसऱ्या संघाला उर्वरित षटकांत किती धावा काढायला हव्यात, ते काढता यायचे. या पद्धतीचा तोटा हा होता, की ही पद्धत अगोदरच्या खेळाची स्थिती लक्षात घेत नसे. तसेच, हे सूत्र फक्त धावांवर आधारलेले होते. किती खेळाडू बाद व्हायचे आहेत, याचा यात विचार केला जात नसे.
या सर्व अनुभवांमुळे, व्यत्ययानंतर खेळ सुरू झाल्यास नवे लक्ष्य निःपक्षपातीपणे पुनः ठरवणे, हे एक मोठे आव्हान ठरले आहे. १९९२मधील एकदिवसीय क्रिकेट विश्वचषक स्पर्धेच्या उपांत्य फेरीच्या वर उल्लिखित सामन्यातील घटनेनंतर आंतरराष्ट्रीय क्रिकेट परिषदेने (आयसीसी) गणितज्ञांना या बाबतीत अधिक चांगली पद्धत शोधण्याचे जागतिक स्तरावर आवाहन केले. त्यानुसार, एफ. सी. डकवर्थ (जन्म: २६ डिसेंबर, १९३९) आणि ए. जे. लुईस (जन्म: २५ फेब्रुवारी, १९४२ ) या अनुक्रमे संख्याशास्त्र आणि गणित या क्षेत्रांतील दोन इंग्लिश तज्ज्ञांनी एकत्रितपणे एक नवी पद्धत विकसित केली. त्यांनी या समस्येवर तोडगा काढताना संघाला लक्ष्य गाठण्यासाठीच्या दोन घटकांचा, म्हणजे उर्वरित षटके आणि हाती असलेले गडी, यांचा प्रामुख्याने विचार केला गेला पाहिजे अशी मूलभूत भूमिका घेतली. (ही भूमिका पूर्वी दुर्लक्षित केली गेली होती.)
१९९२मधील एकदिवसीय क्रिकेट विश्वचषक स्पर्धेच्या उपांत्य फेरीच्या वर उल्लिखित सामन्यातील घटनेनंतर आंतरराष्ट्रीय क्रिकेट परिषदेने (आयसीसी) गणितज्ञांना या बाबतीत अधिक चांगली पद्धत शोधण्याचे जागतिक स्तरावर आवाहन केले. त्यानुसार, एफ. सी. डकवर्थ (जन्म: २६ डिसेंबर, १९३९) आणि ए. जे. लुईस (जन्म: २५ फेब्रुवारी, १९४२ ) या अनुक्रमे संख्याशास्त्र आणि गणित या क्षेत्रांतील दोन इंग्लिश तज्ज्ञांनी एकत्रितपणे एक नवी पद्धत विकसित केली. त्यांनी या समस्येवर तोडगा काढताना संघाला लक्ष्य गाठण्यासाठीच्या दोन घटकांचा, म्हणजे उर्वरित षटके आणि हाती असलेले गडी, यांचा प्रामुख्याने विचार केला गेला पाहिजे अशी मूलभूत भूमिका घेतली. (ही भूमिका पूर्वी दुर्लक्षित केली गेली होती.)
खेळाच्या कुठल्याही अवस्थेत, फलंदाजी करणाऱ्या संघाची धावसंख्या ही मुख्यतः दोन घटकांवर किंवा ‘संसाधनां’वर अवलंबून असते. ही संसाधने म्हणजे बाद न झालेल्या गड्यांची संख्या आणि उर्वरित षटकांची संख्या ह्या दोन्ही गोष्टी लक्षात घेणे गरजेचे आहे. कारण, समजा एका सामन्यात आपले लक्ष्य गाठण्यासाठी एखाद्या संघाची पन्नासांपैकी वीस षटके उरली आहेत आणि त्यांचा एकही गडी बाद झालेला नाही. दुसऱ्या अशाच सामन्यात तेच लक्ष्य गाठणाऱ्या संघाची वीस षटके उरली आहेत, पण त्यांचे फक्त दोन गडी बाकी आहेत. अशा परिस्थितीत, लक्ष्य गाठले जाण्याची शक्यता पहिल्या सामन्यात अर्थातच अधिक आहे. दोन्ही ठिकाणच्या वेगवेगळ्या परिस्थितीचा विचार गणिताद्वारे लक्ष्य निश्चित करताना करायला हवा. त्यामुळे ती पद्धत कोणत्याही परिस्थितीत वापरता येईल, कुठल्याही संघास अवास्तव फायदा देणारी नसेल, प्रथम फलंदाजी करणाऱ्या संघाच्या धावगतीपासून ती स्वतंत्र असेल, तिचा वापर साध्या गणकयंत्राने करता येईल आणि ती खेळाडू, पंच, प्रशिक्षक, व्यवस्थापक, समीक्षक, वार्ताहर आणि प्रेक्षक, या सर्वांस सहज समजू शकेल अशी असावी, हा दृष्टिकोन त्यांनी ठेवला. डकवर्थ आणि लुईस यांच्या पद्धतीत संसाधनांच्या वापराची टक्केवारी लक्षात घेतली जाते.
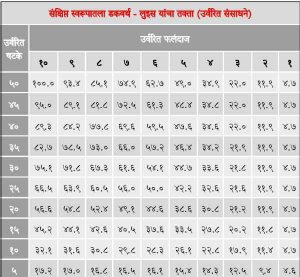
डकवर्थ आणि लुईस यांनी तोपर्यंतच्या जवळपास सर्व प्रमुख एकदिवसीय सामन्यांत झालेल्या धावा, टाकलेली षटके आणि बाद झालेले गडी यांच्या आकडेवारीचा सखोल अभ्यास करून घातांकांवर (एक्सपोनेंशियल) आधारलेले एक गणिती सूत्र मांडले. या सूत्रात त्यांनी, एकदिवसीय सामन्यांत झालेल्या धावसंख्यांची सरासरी, सामन्यातल्या पूर्ण झालेल्या विविध षटकांपर्यंतच्या धावांची सरासरी, बाकी असलेल्या षटकांत होऊ शकणाऱ्या धावांची सरासरी, बाद झालेल्या गड्यांची संख्या, अशा विविध घटकांचा समावेश केला. त्यानंतर आपल्या सूत्रानुसार, उर्वरित षटके आणि उर्वरित गडी यांवर आधारलेले, सहज वापरता येतील असे तक्ते त्यांनी तयार केले. या तक्त्यांवरून उर्वरित संसाधनांच्या वापरांची टक्केवारी काढली जाते आणि त्यावरून छोटे गणित करून नवे लक्ष्य ठरवले जाते.
 डकवर्थ आणि लुईस यांची ही गणिती पद्धत १९९७ सालाच्या सुमारास काही आंतरराष्ट्रीय सामन्यांत व इंग्लंडमधील स्थानिक एकदिवसीय सामन्यांच्या स्पर्धांत चाचणी म्हणून वापरली गेली आणि ही पद्धत तर्कशुद्ध लक्ष्य सुचवेल याची खात्री केली गेली. उदाहरणार्थ, डकवर्थ लुईस पद्धतीने जर गणित केले गेले असते, तर वर उल्लेख केलेल्या सामन्यात दक्षिण आफ्रिकेला जिंकण्यासाठी एका चेंडूत पाच धावांचे लक्ष्य दिले गेले असते. हे नक्कीच व्यावहारिक होते. डकवर्थ आणि लुईस यांनी आपले हे सर्व संशोधन इंग्लंडमधून प्रसिद्ध होणाऱ्या ‘जर्नल ऑफ द ऑपरेशनल रिसर्च सोसायटी’च्या नियतकालिकात १९९८ साली, आठ पानी शोधनिबंधाद्वारे प्रसिद्ध केले.
डकवर्थ आणि लुईस यांची ही गणिती पद्धत १९९७ सालाच्या सुमारास काही आंतरराष्ट्रीय सामन्यांत व इंग्लंडमधील स्थानिक एकदिवसीय सामन्यांच्या स्पर्धांत चाचणी म्हणून वापरली गेली आणि ही पद्धत तर्कशुद्ध लक्ष्य सुचवेल याची खात्री केली गेली. उदाहरणार्थ, डकवर्थ लुईस पद्धतीने जर गणित केले गेले असते, तर वर उल्लेख केलेल्या सामन्यात दक्षिण आफ्रिकेला जिंकण्यासाठी एका चेंडूत पाच धावांचे लक्ष्य दिले गेले असते. हे नक्कीच व्यावहारिक होते. डकवर्थ आणि लुईस यांनी आपले हे सर्व संशोधन इंग्लंडमधून प्रसिद्ध होणाऱ्या ‘जर्नल ऑफ द ऑपरेशनल रिसर्च सोसायटी’च्या नियतकालिकात १९९८ साली, आठ पानी शोधनिबंधाद्वारे प्रसिद्ध केले.
औपचारिकरीत्या १९९९ साली आंतरराष्ट्रीय क्रिकेट परिषदेने एकदिवसीय सामन्यात पावसाने किंवा इतर कारणाने व्यत्यय आल्यास धावांचे लक्ष्य ठरवण्यासाठी डकवर्थ/ लुईस यांची सदर पद्धत प्रमाणित (स्टँडर्ड) पद्धत म्हणून मान्य केली आणि एकदिवसीय क्रिकेट विश्वचषक स्पर्धेत, १९९९मध्ये ती प्रथमच वापरली गेली. पहिल्या किंवा दुसऱ्या डावात एकदा किंवा अधिक वेळा व्यत्यय येण्यासारख्या परिस्थितीतही ही डकवर्थ लुईस पद्धत मूळ स्वरूपात २००३ सालापर्यंत वापरली गेली. मात्र, तोपर्यंत एकदिवसीय सामन्यात काढल्या जाणाऱ्या धावांचे प्रमाण वाढू लागल्याचे आढळून आल्याने डकवर्थ/ लुईस यांनी त्यांच्या गणिती प्रारूपात आवश्यक असा बदल केला आणि एक सुधारित पद्धत मांडली. या पद्धतीला डकवर्थ/ लुईस पद्धतीची व्यावसायिक (प्रोफेशनल) आवृत्ती म्हटले जाते. सर्व आंतरराष्ट्रीय आणि काही राष्ट्रीय एकदिवसीय सामन्यांत ही सुधारित पद्धत वापरणे २००४ सालापासून अनिवार्य केले गेले आहे. तिच्या वापरासाठी संगणक आवश्यक ठरतो. मात्र, इतर पातळ्यांवरील सामन्यांत किंवा ही आवृत्ती वापरण्याची सुविधा उपलब्ध नसल्यास, पूर्वीची प्रमाणित (स्टँडर्ड) पद्धत वापरण्याची मुभा दिली गेली आहे.
डकवर्थ / लुईस प्रमाणित पद्धतीच्या वापराचे एक उदाहरण म्हणून श्रीलंका विरुद्ध दक्षिण आफ्रिका हा २००३ मधील एकदिवसीय क्रिकेटच्या विश्वचषक स्पर्धेतील एक सामना बघू या. श्रीलंकेने पहिल्यांदा फलंदाजी करून ५० षटकांत २६८ धावा केल्या. याचा अर्थ, श्रीलंकेने शंभर टक्के संसाधने वापरली. म्हणजे (स१ ) १०० टक्के. उत्तरादाखल दक्षिण आफ्रिकेने ४५ षटकांत ६ गडी बाद २२९ धावा केल्या असताना पावसामुळे खेळ थांबला. डकवर्थ/ लुईस यांच्या तक्त्याप्रमाणे दक्षिण आफ्रिकेकडे, उर्वरित ४ गडी आणि उर्वरित ५ षटके या स्थितीत १४.३ टक्के संसाधने उरली होती. म्हणजे दक्षिण आफ्रिकेने वापरलेल्या संसाधनांची टक्केवारी ही (स२) = १०० – १४.३ = ८५.७ टक्के इतकी होती. आता स१ हे स२पेक्षा अधिक असल्यामुळे जिंकण्यासाठी दक्षिण आफ्रिकेचे नवे लक्ष्य [ (स२/स१) × (श्रीलंकेच्या धावा)] + १ [(८५.७/१००) × २६८] + १ = २२९.६ + १ = २३० (स्थूलांकन करून) असे होते. मात्र, दक्षिण आफ्रिकेने २२९ धावा केल्या आणि तो सामना बरोबरीत सुटला.
 आता आणखी एक उदाहरण बघू या. आता पहिला डावही पूर्ण न झाल्यामुळे इथे गणित थोडेसे वेगळे आहे. भारताने श्रीलंकेच्या विरुद्ध एका सामन्यात प्रथम फलंदाजी सुरू करून, २९ षटकांत ३ गडी बाद ११९ धावा केल्या असताना पाऊस आला आणि सामना २९ षटकांचा असावा, असा निर्णय घेतला गेला. त्यामुळे डकवर्थ/ लुईस पद्धतीनुसार श्रीलंकेसाठी लक्ष्य ठरवले गेले ते असे. भारताकडे सुरुवातीला असलेली संसाधने = १०० टक्के. पावसामुळे खेळ थांबला तेव्हा म्हणजे, उर्वरित ७ गडी आणि उर्वरित २१ षटके असताना तक्त्याप्रमाणे भारताकडे असलेली संसाधने होती ५०.६ टक्के. त्यानुसार भारताने वापरलेली संसाधने ( स १ ) = १०० – ५०.६ = ४९.४ टक्के. आता तक्त्याप्रमाणे डाव सुरू करताना शून्य गडी बाद आणि २९ षटके या स्थितीत श्रीलंकेकडे असलेली संसाधने (स२) ७३.५ टक्के. स२ हे सरपेक्षा अधिक असल्यामुळे जिंकण्यासाठी श्रीलंकेचे नवे लक्ष्य = [(स२ स१) × (सरासरी =[(७३.५ – ४९.४) ×धावा/१००)] + भारताच्या धावा + १ (२४५/१००)] + ११९ + १ १७८ (स्थूलांकन करून). म्हणजे श्रीलंकेला सामना जिंकण्यासाठी २९ षटकांत १७८ धावा काढण्याची गरज होती. प्रत्येक षटकामागचे जवळपास ६ धावांचे हे निर्धारित लक्ष्य वाजवी आणि चुरशीचे होते. इथे सर्वसाधारणपणे ५० षटकांत २४५ धावा काढल्या जातात हे डकवर्थ/ लुईस पद्धतीतील, तोपर्यंत उपलब्ध झालेल्या सामन्यांच्या आकडेवारीच्या अभ्यासातून काढले गेलेले गृहीतक आहे.
आता आणखी एक उदाहरण बघू या. आता पहिला डावही पूर्ण न झाल्यामुळे इथे गणित थोडेसे वेगळे आहे. भारताने श्रीलंकेच्या विरुद्ध एका सामन्यात प्रथम फलंदाजी सुरू करून, २९ षटकांत ३ गडी बाद ११९ धावा केल्या असताना पाऊस आला आणि सामना २९ षटकांचा असावा, असा निर्णय घेतला गेला. त्यामुळे डकवर्थ/ लुईस पद्धतीनुसार श्रीलंकेसाठी लक्ष्य ठरवले गेले ते असे. भारताकडे सुरुवातीला असलेली संसाधने = १०० टक्के. पावसामुळे खेळ थांबला तेव्हा म्हणजे, उर्वरित ७ गडी आणि उर्वरित २१ षटके असताना तक्त्याप्रमाणे भारताकडे असलेली संसाधने होती ५०.६ टक्के. त्यानुसार भारताने वापरलेली संसाधने ( स १ ) = १०० – ५०.६ = ४९.४ टक्के. आता तक्त्याप्रमाणे डाव सुरू करताना शून्य गडी बाद आणि २९ षटके या स्थितीत श्रीलंकेकडे असलेली संसाधने (स२) ७३.५ टक्के. स२ हे सरपेक्षा अधिक असल्यामुळे जिंकण्यासाठी श्रीलंकेचे नवे लक्ष्य = [(स२ स१) × (सरासरी =[(७३.५ – ४९.४) ×धावा/१००)] + भारताच्या धावा + १ (२४५/१००)] + ११९ + १ १७८ (स्थूलांकन करून). म्हणजे श्रीलंकेला सामना जिंकण्यासाठी २९ षटकांत १७८ धावा काढण्याची गरज होती. प्रत्येक षटकामागचे जवळपास ६ धावांचे हे निर्धारित लक्ष्य वाजवी आणि चुरशीचे होते. इथे सर्वसाधारणपणे ५० षटकांत २४५ धावा काढल्या जातात हे डकवर्थ/ लुईस पद्धतीतील, तोपर्यंत उपलब्ध झालेल्या सामन्यांच्या आकडेवारीच्या अभ्यासातून काढले गेलेले गृहीतक आहे.
वयोमानाने डकवर्थ आणि लुईस निवृत्त झाल्याने प्रा. एस. स्टर्न हे सदर पद्धतीवर पूर्णवेळ कार्य करत असून त्यांनी त्यात नवी भर घातली आहे. म्हणून नोव्हेंबर नोव्हेंबर २०१४पासून याला डकवर्थ/ लुईस/स्टर्न (डीएलएस) पद्धत असे म्हटले जाते. त्यानुसार मोठ्या धावसंख्येचा पाठलाग करताना दुसऱ्या संघाने धावांची गती मोठी ठेवणे आवश्यक असेल, परंतु गडी किती बाद होतात याला महत्त्व नाही. ही नवी पद्धत २०१५च्या विश्वचषक स्पर्धेत वापरली गेली होती आणि इंग्लंडमधील ३० मे ते १४ जुलै, २०१९ दरम्यान होत असलेल्या एकदिवसीय विश्वचषक स्पर्धेतही ती वापरली जात आहे. या सुधारित आवृत्तीत मागील चार वर्षांतील ७०० एकदिवसीय सामने, ४२८ टी२० सामने म्हणजे २,४०,०००हून अधिक वैध चेंडूंवर काढलेल्या धावांचा विचार केला गेला आहे. जर ही पद्धत वापरून संघ विजयी झाला असल्यास त्याची नोंद अशी केली जाते: ‘संघ य २५ धावांनी विजयी (डीएलएस पद्धत) .
आयसीसीने वेळोवेळी डकवर्थ/ लुईस/ स्टर्न पद्धतीचे, उर्वरित संसाधने दाखवणारे तक्ते असणाऱ्या पुस्तिका प्रसिद्ध केल्या आहेत. या तक्त्यांमुळे उपलब्ध षटके किंवा चेंडूंच्या प्रमाणात सुधारित लक्ष्य ठरवण्यास मदत होते. हे तक्ते देताना त्यांबरोबर त्यांच्या वापराची विविध परिस्थितींसाठी उदाहरणेदेखील दिली आहेत. ही पद्धत थोडी सुधारून टी २० सामन्यांसाठीही वापरली जाते. मात्र टी२० सामन्यांत षटकांची संख्या आणखी कमी असल्यामुळे फलंदाजीचा रोख अधिक आक्रमक असतो. त्यामुळे गडी हाती असणे हे कमी महत्त्वाचे ठरते. या खेळाचे काही नियमही वेगळे आहेत. डकवर्थ/ लुईस यांची ही पद्धत मुळातच ५०-५० षटकांच्या डावांसाठी तयार केली गेली होती. तेव्हा २०-२० षटकांच्या डावासाठी त्यात आमूलाग्र बदल केले जावेत किंवा त्यासाठी वेगळी पद्धत विकसित करावी, असे मत पुढे आले असून त्यावर विचार चालू आहे.
क्रिकेटसारख्या अनिश्चित खेळाचे भवितव्य कुठल्याही गणिती पद्धतीने ठरवल्यास त्यात काही दोष राहणे स्वाभाविक आहे. डकवर्थ/ लुईस पद्धतही त्याला अपवाद नाही. उदाहरणार्थ, पाऊस येण्याची शक्यता लक्षात घेऊन नंतर फलंदाजी करणाऱ्या संघाकडे अधिक गडी हाती असणे हे फायद्याचे ठरू शकते. षटकांच्या संख्येप्रमाणे क्षेत्ररक्षणावर असलेले निर्बंध किंवा पॉवरप्ले नियम, हे या पद्धतीत लक्षात घेतले गेलेले नाहीत. तसेच, ही पद्धत वाटते तितकी लोकाभिमुख नाही. अर्थातच, या पद्धतीवर मोठ्या प्रमाणात शैक्षणिक आणि क्रिकेट वर्तुळांतदेखील संशोधन चालू असून या मर्यादांवर तोडगे सुचवले जात आहेत.
हवेतून जाताना किंवा खेळपट्टीवर पडल्यावर चेंडूची दिशा कशी बदलते, कसोटी सामन्यात विजयाची शक्यता वाढवण्यासाठी डाव केव्हा घोषित करावा, फलंदाजीचा क्रम वेगवेगळ्या प्रकारच्या सामन्यांत कसा ठरवावा, अशा क्रिकेटशी संबंधित विविध पैलूंबाबत गणिताच्या अनेक शाखांचा वापर केला गेला आहे आणि तो अधिक सखोल करणे शक्य आहे. विपुल प्रमाणात उपलब्ध असलेली क्रिकेटबद्दलची आकडेवारी ही तर गणितीय विश्लेषणासाठी एक खाणच आहे. या माहितीच्या विश्लेषणातून बहुविध आणि रंजक माहिती पुढे येऊ शकते, सामन्याच्या निकालाचा अंदाज वर्तवला जाऊ शकतो.
किंबहुना या प्रकारे क्रिकेटच नव्हे, तर जागतिक, राष्ट्रीय, राज्य आणि स्थानिक पातळीवर आयोजित होणाऱ्या इतर मैदानी किंवा बैठ्या खेळांविषयी प्रचंड प्रमाणात उपलब्ध असलेली माहिती आणि आकडेवारीसुद्धा विविध प्रकारच्या गणितांवर आधारलेल्या संशोधनाचा विषय होऊ शकते आणि त्यातून क्रीडागणिती किंवा क्रीडासांख्यिकी अशी चांगली व्यावसायिक कारकीर्द घडवली जाऊ शकते.
-विवेक पाटकर
गणिततज्ज्ञ
vnpatkar2004@yahoo.co.in
मराठी विज्ञान परिषदेच्या ‘पत्रिका’ या मासिकातील हा पूर्वप्रकाशित लेख






Leave a Reply