To every problem, there is a most simple solution. हे चिंट्या जितके सहज म्हणाला, तितके सहज उत्तर मिळेल याची कुणालाच खात्री नव्हती. पण शोधले तर पाहिजेच! त्याशिवाय गत्यंतर नव्हते…

**************************
आत्ता पर्यंत: टीम पुणे त्रिकोणी ग्रहावर उतरली. यानातून बाहेर येऊन शहराकडे निघाली. वाटेत एक नदी आडवी आली. बोट बरोबर समोरच्या तीरावर असलेल्या कॅनॉल मध्ये न्यायची होती. स्टीअरिंग जॅम झाले होते आणि प्रवाह खूपच जोरात होता. बोट कॅनॉल मधे नाही नेता आली तर…
गोष्टीचा आधीचा भाग…. इथे टिचकी मारा
**************************
तिकीटघरात टेबलावर बसून सगळे आयडिया लढवू लागले. बोटीला स्टीयरिंग आहे तर मग काय प्रॉब्लेम आहे? प्रवाहामुळे बोट ओढली गेली तर स्टीयरिंगने ने जागेवर आणता येणार नाही का? सायलीला समजावून सांगणे नेहाला जड जात होतं. न्यूटनच्या नियमाप्रमाणे F = m × a. पाणी खूप असल्यामुळे त्याचे वस्तुमान (m) खूप आहे, त्यामुळे पाण्याच्या प्रवाहाचे बल (Fr) खूप जास्त आहे. त्या मानाने बोटीची बल (Fb) – शक्ती काहीच नाही… सायकल घसरते तेव्हा हँडल वळवून उपयोग होतो का?
चिंट्याने काही कँलक्युलेशन पुढे केले. पण त्यातल्या गृहीत तपासल्यावर, हेच का, तसे का असे विचारल्यावर चूक लक्षात आली… सोल्युशन एव्हढ सिम्पल नाही तर… मनातल्या मनात पोयरोला म्हणाला. Use your little grey cells, mon ami (माझ्या मित्रा)… पोयरोने हसून उत्तर दिले.
अगदी गणिताचा वार्षिक परीक्षा देतोय असे वाटतंय, सायली पुटपुटली, काय करायचे हे सुचतच नाही… नेहाने तिला धीर दिला… म्हणूनच तर सांगतात, पेपर सोडवताना प्रश्न समजून घ्या, काय विचारले ते आधी समजून घ्या…
करेक्ट! नेहा मोठ्याने म्हणाली. तिघेही तिच्याकडे बघू लागले…
प्रश्न नीट समजून घ्या… आपल्याला काय शोधायचे आहे ते आधी स्पष्ट करू. नेहाने कागद पेन घेतले. ही नदी…, दोन समांतर रेषा काढत म्हणाली. आपल्याला इथे पोहोचायचे आहे. वरच्या रेषेवर एक बिंदू काढला, त्याला ‘A’ लेबल लावले. आपण B इथे आहोत, A च्या बरोबर समोर B काढला.
नदीच्या प्रवाहामुळे आपण उजवीकडे ओढले जाऊ. जितके उजवीकडे, तेव्हडीच डावीकडून सुरुवात करायला हवी. नेहाने एक बाण A पासून उजवीकडे जाणारा काढला. त्याचा समोर B कडून डावीकडे जाणार बाण काढला. प्रवाहामुळे आपल्याला B पासून जाण्या ऐवजी… तिने Bच्या डावीकडे X… इथून जायला हवे.
बोटीची दिशा सरळच असेल. X च्या बरोब्बर समोरच्या तीरावर Y काढला. बोटीने XY जाण्याचा प्रयत्न केला पाहिजे, म्हणजे प्रत्यक्षात, प्रवाहामुळे A पाशी पोहचेल. आपली बोट XA रेषे वरून जाईल. XA जोडल्यावर एक काटकोन त्रिकोण तयार झाला… म्हणजे आपल्याला BX हे अंतर शोधायचे आहे!
ये तो अपणेको माहितीच था!! चिंट्याने हिंदीची वाट लावली… पण कैसे? ये प्रश्न शोधणेका है ना!
उजवीकडे अंतर किती? प्रवाहाचा वेग गुणिले बोटीचा पाण्यातला वेळ… पाण्यातला वेळ म्हणजे, नदीची रुंदी AB भागीले बोटीचा वेग… बोटीचा वेग बोटीवर लिहिलाय… 4m/s. म्हणजे आपल्याला नदीची रुंदी किंवा AB शोधायची आहे. आणि BX साठी प्रवाहाचा वेग! नेहाने प्रश्न स्पष्ट केला.
प्रवाहाचा वेग आणि AB शोधणे फारच सोपं आहे . चला माझ्या बरोबर. सॅमीने चार्ज घेतला. चिंट्या, तुझा स्विस पॉकेट चाकू दे…आता सॅमीने स्पीड पकडला.
सगळे बाहेर आले. सॅमीने झुडुपाच्या लाल पांढरी फुलं असलेल्या 10-12 जाड फांद्या तोडून आणल्या. बोटीतून हुक असलेली काठी घेतली. चिंट्या, काठीवर फुटपट्टी सारख्या खूणा आहेत, त्या तुझ्या कीचेनला असलेल्या टेपनी तपासून घे. मग या खांबा पासून, डावीकडे 10, 20, 30 आणि 40 मीटरवर खुणा कर. नेहा तू खांबा जवळ, मग सायली आणि तिसरा चिंट्या असे उभे राहा… चिंट्याच्या पुढे मी शेवटी उभा राहतो. मी एक एक करत ह्या फांद्या पाण्याच्या प्रवाहात टाकीन. पाण्यात पडताच तुम्ही फोनवर स्टॉपवॉच चालू करा. फांदी तुमच्या बरोबर समोर येताच वेळ नोंदवा… चिंट्या तू पहिला असशील, म्हणजे फांदीला 10 मीटर जायला वेळ किती हे तुला उत्तर मिळेल. सायली तू मधे, म्हणजे 20 मीटर, आणि नेहा तू तिसरी म्हणजे 30 मीटर जाण्याचा वेळ मिळेल. सर्व रिडींग नोंदवून घ्या. एव्हरेज काढून बऱ्यापैकी अचूक प्रति सेकंद वेग मिळेल!
ब्रि–ल्ली–यं–ट!!!! सॅमी, तुला एक मोठं कॅडबरी चॉकलेट माझ्या कडून गिफ्ट – नेहा आनंदाने म्हणाली.
प्रवाहाचा वेग 1.5 m/s होता.
(वाचकहो, तुमच्या आवडीने दुसरा वेग गृहीत धरला तर चालेल :-)पण पुढचं गणित तुम्हाला करावं लागेल.)
चला आता दुसरा भाग, नदीची रुंदी AB शोधूया!
चिंट्या, तू 30 मीटर मोजले होते त्या खुणेवर ही काठी सरळ उभी धरून थांब. तो पॉईंट C आहे असे म्हणू. म्हणजे BC 30 मीटर आहे. त्याचा पुढे एक मीटरवर सॅमीने अजून एक खूण केली…. हा पॉईंट D. CD एक मीटर आहे.
आता सॅमीने नदी किनाऱ्याला काटकोनात एक सरळ लांब रेघ काढली, आणी पुन्हा D पाशी येऊन या रेघे वर चालू लागला. दर तीन चार पावलांनी वळून चिंट्याचा काठीकडे बघत होता. खाली बसून काठी आणि त्या पलीकडे काहीतरी बघत होता… नेहाची ट्यूब पेटली. तिने धावत जाऊन बोटीतली दुसरी काठी आणली. सॅमी थांबताच तिथे काठी रेघे वर ठेवून उभी धरली. सॅमी बसून बघायचा आणि पुन्हा पुढे जायचा. एके ठिकाणी तो एक दोन पावलं मागे आला. सुरेख, सॅमी म्हणाला, नेहाने धरलेली काठी थोडी ऍडजस्ट केली, आणि समाधानाने म्हणाला, ही काठी, चिंट्याच्या हातातली काठी आणि पलीकडचा खांब – तिन्ही सरळ एका रेषेत आहेत. हा पॉईंट E…
नेहाने काठीवरच्या खुणा वापरून DE हे अंतर मोजले. ते 8 मीटर होते!
(वाचकहो, इथेही दुसरा आकडा चालेल :-)फक्त वाजवीपणा सांभाळा!)
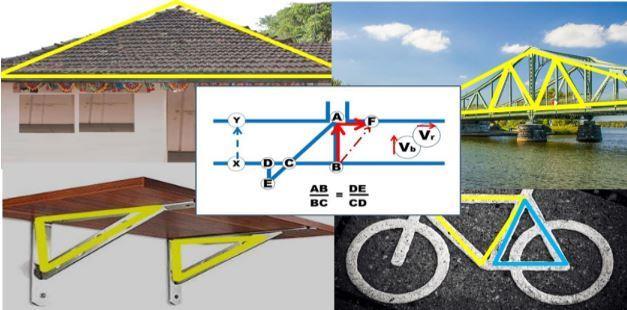
सगळे पुन्हा तिकीटघरातल्या टेबला भोवती बसले. सॅमीने नेहाने काढलेल्या चित्रावरच गणित केलं. AB ही नदीची रुंदी नेहाने दाखवली होती. सॅमीने B पासून, नदीच्या काठावर डावीकडे C बिंदू काढला आणि 30m लिहिले. पुढे D बिंदू मांडुन 1m लिहिले. D पासून काटकोनात रेघ काढली. आता A आणि C जोडून एक मोठी रेघ काढली आणि त्या रेघेनी D पासून काढलेल्या रेघेला छेदले, छेद बिंदूला E लेबल दिले. DE च्या बाजूला 8m लिहिले. (वाचकहो: आकृती कोलाज मध्ये आहे.)
ABC आणि DCE समकोन त्रिकोण आहेत – सॅमी सांगू लागला. म्हणजे AB / BC = DE / CD, तेव्हा AB = DE / CD × BC,म्हणजेच AB = 8/1 × 30 = 240m = नदीची रुंदी!!!!
टाळ्यांचा कडकडाट आणि पाठोपाठ सॅमीच्या पाठीवर थाप पडल्या! त्यांचा चेहऱ्यावर आनंद स्पष्ट दिसत होता…
आता पुढचा भाग. X किधर है? बोट कुठून पाण्यात न्यायची? बोटीचा वेग 4m/s, म्हणजे 240m ची नदी, 240/4 = 60s मधे नदीचे अंतर बोट पार करेल. नदीचा प्रवाह 1.5m/s, म्हणजे 60s मधे पाण्यावरची वस्तू 60 × 1.5 = 90m जाईल! म्हणजे आपल्याला B पासून 90m मोजून तिथून क्रॉस करावं लागेल. आपण बोट सरळ समोरच्या किनाऱ्याकडे XY नेऊ, पुढचे काम प्रवाह करेल आणि आपण XA जाऊन A पाशी पोहोचू, कॅनॉल मधे प्रवेश करू…
झकास, लै खास…, पुन्हा एकदा टाळ्या, पाठीवर थापांचा पाऊस झाला.
आता सगळ्यांना तात्काळ निघायचे होते. पण नेहाने थांबवले. पुन्हा एकदा पद्धत आणि गणित तपासण्याचा आग्रह केला. काय बोअर आहेस तू… पण नेहाने ऐकलं नाही.
सायली आणि चिंट्या तिला गणित समजावून सांगू लागले, पटवू लागले… मधेच नेहा त्यांना गुगली बॉल टाकत होती… AB / BC = DE / CD का? AB / BC = CD / DE का नाही? समकोण त्रिकोणाचा संगत कोन आणि त्यांचा बाजू बघितल्या पाहिजे ना! चिंट्याने समजावले. शेवटी ती तयार झाली.
सॅमीने हळूच नेहाला विचारले – वेळ घालवण्याचे कारण? नेहा हसली. दोघे थोडे उतावळे आहेत आणि एक्ससाईट होतात. त्यांना थोडा वेळ देणे आवश्यक होतं.
आणि परीक्षेत गणित ‘सुटलं’च्या आनंदात आपण मागे वळून बघत नाही, नाही का? बघितलं तरी चूका दिसतात? मार्क आल्यावर कळतं… आणि वर बोलणी… वेंधळ्या सारख्या चूका करून मार्क घालवल्या बद्दल… यातून आपण काय शिकतो?
केलेले काम पुन्हा तपासावे, चुका दिसल्या नाही तर उलट सुलटं करून पाहावं, गृहीत चॅलेंज करून पहावी… पेपर मधले मार्क आणि बोलणी जीवावर उठत नाही, पण आयुष्यातल्या चुका… बोटीत शांत आणि सांभाळून हालचाल करावी लागते… एक्साईटमेंट मुळे ताबा सुटू शकतो… बोट उलटली तर?… वेळ घालवणे नक्कीच नाही…
मुलांनी आपल्या तिरावरच्या खांबा पासून 90m मोजले. तिथे त्यांना बोटीच्या चाकाच्या जुन्या खुणा दिसल्या. समोर तीरावर झाडीतून डोकावणारा अजून एक लाल-पांढरा खांब दिसला. आपण केलेले सर्व गणित बरोबर असल्याची पुष्टी मिळाली.
सॅमी तू आणि सायली त्या हुकच्या काठ्या घेऊन पुढे बसा. कॅनॉलच्या तोंडाशी दोन्हीकडे खांब आहेत. बोटीतून बाहेर न वाकता, हुकने खांब पकडा आणि बोट ओढून घ्या कॅनॉल मधे. गणित बरोबर असलं तरी प्रत्यक्षात किंचित इकडे तिकडे होऊ शकते… चिंट्या, गरज लागली तर दोरीचा फास करून खांबावर टाक, हे फक्त तुलाच जमेल. दुसरं टोक बोटीचा पुढंच्या हुकला आत्ताच बांध…
चलो टीम पुणे. मिशन बोलावताय…
***** थोड्या वेळाने ********
त्रिकोण नगरात तुमचे स्वागत आहे.
बोटीच्या धक्क्यावर एक वयस्कर, पण ताठ गृहस्थ उभे होते. लांब पांढरी शुभ्र दाढी, मागे वळलेले केस. एक पांढरे शुभ्र वस्त्र, प्राचीन ग्रीक लोकांसारखे घातले होते.
माझं नाव एरेटॉसथिनिस (Eratosthenes). मी तुम्हचा इथला गाईड आहे. पण आधी आपण हॉटेलवर जाऊ. थोडा आराम करून फ्रेश व्हा. नाश्ता करून शहराचा फेरफटका करू…
… ग्रहावरच्या महासागरात तीन खंड आहेत. तीनही त्रिकोणी आहेत. पहिला समभुज, दुसरा समद्विभुज आणि तिसरा विषमभुज. ग्रहावर एकच देश आहे आणि त्याची राजधानी त्रिकोण नगर. त्रिकोण नगराची रचना सुद्धा समभुज आहे. लघुकोन, विशालकोन आणि काटकोन अशी तीन उपनगर आहेत. तीनही उपनगरांच्या मधे आणि खंडाच्या मध्य बिंदूवर पायथोगोरसचा पुतळा आहे…
म्हणजे भूमिती आणि भूगोल एकाच वेळी शिकवता येईल… नेहा हसून म्हणाली. एरेटॉसथिनिसनी पण हसून दाद दिली – आम्हाला त्रिकोण आकाराचे फार आकर्षण आणि आदर आहे हे खरे.
आमचे पूर्वज प्रथम या ग्रहावर आला तेव्हा त्यांचाकडे फारसे साधन नव्हते. जंगल साफ करून लाकडाचे, बांबूचे घरं बांधून राहात होते. पण या ग्रहावर अधुमधून फारच जोरात वारं वाहतं. चौकोनी आकाराचे, चार भीतीचे घर छान उभे राहायचे, पण वाऱ्याचा तिरका जोर लागला की भुईसपाट व्हायचे! तेव्हा त्रिकोणी बांधणीच्या “ट्रस” फ्रेमचा शोध लागला. घर वाऱ्यापुढे टिकू लागले. पुढे पिरॅमिड आकाराची घरं अजून चांगली टिकतात हे लक्षात आलं. त्याचा प्रभाव आजही दिसतो…
इजिप्तच्या पिरॅमिड पण तीन चार हजार वर्षे जुनी आहेत, पण सगळं टिकलंय. नेहा म्हणाली. होय. कारण त्रिकोण हा सर्वात ताठर आणि कडक आकार आहे. प्रचंड जोर लावला, उभा आडवा तिरका… तरी आपला आकार धरून ठेवतो.
आपण हा गुण अनेक ठिकाणी वापरतो. अगदी सायकल पासून ते नदीवरचा छोट्या मोठ्या पुला पर्यंत. मोबाईलचे, विद्युत पूरवठ्याचे मोठे मोठे टॉवर्स पण नीट बघितले तर अनेक त्रिकोणांची जोड केलेली दिसते.
घरात सुद्धा भिंतीवर रॅक लावता तेव्हा त्याला खाली तिरका आधार असतो. अशा त्रिकोणी आधार देणाऱ्या बांधणीला “ट्रस (Truss)” म्हणतात. इतका प्रचंड उपयोग आहे, त्यामुळे आम्हाला त्रिकोण आकाराचे आकर्षण आणि आदर आहे आणि हे तुम्हाला सर्वत्र दिसेल. इथे प्रत्येक बांधकामात, रस्त्यांच्या आखणी मधे, त्रिकोणाच्या एक तरी प्रमेय स्पष्टपणे दिसेल अशी अपेक्षा असते…
**************************
हा छान विडिओ बघा Strong Structures with Triangles | Design Squad
सावधान! प्रयोग स्वतःच्या जबाबदारीवर…
**************************
फिरत फिरत ते एका मोठ्या चौकात आले, चौकाचे नाव एरेटॉसथिनिस चौक होते. हुबेहूब काकांसारखाच दिसणारा एक मोठा पुतळा चौकात मध्यभागी होता. मुलांनी काकांकडे बघितले, आणि काका थोडे लाजले. तो मी नव्हे. पृथ्वीवरच्या इ.स. पूर्व दुसऱ्या शतकात होऊन गेलेल्या महान ग्रीक खगोलतज्ञाचे हे स्मारक आहे. ह्यांनी घरात बसून, समकोण त्रिकोण आणि त्रिकोणमितिचा (Trigonometry) उपयोग करून पृथ्वीचा परीघ किती हे सांगितले. माझ्या आइ वडिलांना ती गोष्ट इतकी आवडली की त्यांनी माझे नाव तेच निवडले…
काका, ती गोष्ट सांगा ना… मुलांनी आग्रह केला. एरेटॉसथिनिस सांगू लागले…
आणि तेवढ्यात… …
तीन वाजल्याचा अलार्म वाजला आणि नेहाने ब्राउजर बंद केला.
********** क्रमशः *****
शिक्षकांसाठी काही विचार (Suggestions :–) )
- त्रिकोण प्रकार, प्रमेय, गुणधर्म, … आपल्या मित्रांना नदी पार करायला हे ज्ञान आवश्यक आहे.
- प्रॉब्लेम सोडवण्यासाठी उपयुक्त स्ट्रेटजी पूर्वी दिली आहे, (गोष्ट सांगा आणि गणित शिकवा… ३), ती किंवा तुम्ही शिकवलेली स्ट्रेटेजी पुन्हा रिव्हीझन करणे उचित होईल.
- जेव्हा प्रश्न स्पष्टपणे मांडला जातो, समजतो तेव्हाच काय करायचे आहे हे कळते, योग्य कृती आठवेते, प्रश्नाचे उत्तर मिळते, हे आवर्जून सांगा.
- ज्ञानाचा उपयोग सांगितला तर ते जास्त चांगले समजते. विडिओ जरूर दाखवा. अजूनही बरेच आहेत, तुम्हाला आवडेल तो निवडा.
********************
गोष्टीचा पुढचा भाग… लवकरच
********************
— राजा वळसंगकर






Leave a Reply